Visualization of Hybrid Atomic Orbitals
Chemical Bonding
Just as an atom has orbitals that describe the various ways an electron can exist around the nucleus, similarly molecules have orbitals that describe the ways an electron can exist around the nuclei in the molecule. The mathematical computation of orbitals is time-consuming and mathematically complicated. Consequently chemists employ simple approximations to arrive at a qualitative (or perhaps semi-quantitative) description of chemical bonding.
Orbitals associated with molecules are approximated as linear combinations of atomic orbitals from the atoms in the molecule. Recall that an orbital is simply a mathematical function known as a wave function. Each electron is characterized by a wave function that describes the state of the electron. Thus combining orbitals is simply a case of mathematically adding of subtracting the wave functions associated with each orbital to obtain a new wave function (that is, a new orbital).
There are two approaches to implementing this approximation based upon overlap of atomic orbitals. In Molecular Orbital Theory, the various atomic orbitals are directly combined mathematically to obtain a set of molecular orbitals. These molecular orbitals can span the entire molecule, involving orbital contributions from several different atoms.
In Valence Bond Theory, a chemical bond is treated as localized between two atoms. The mathematical combination of atomic orbitals from each atom in the bond produces a bond orbital with electron density concentrated between the two atoms. In practice, a strictly localized approach to bonding does not work in many cases. To remedy this limitation, Valence Bond Theory uses the concept of resonance to account for bonding that simultaneously involves multiple atoms.
Hybrid Orbitals
Suppose one wishes to use Valence Bond Theory to describe a chemical bond between a carbon and a nitrogen atom: C-N. The orbital for the C-N bond is modeled as the mathematical combination of an atomic orbital from the carbon and an atomic orbital from the nitrogen. In this case, the bond is a sigma bond ( σ ) in which electron density is concentrated in the region between the two nuclei. In order to concentrate electron density between the two nuclei, the atomic orbitals from each atom (those orbitals overlapping to form the bond) should be oriented directly toward the other atom.
For this purpose, the basic s, px, py, and pz orbitals are unsatisfactory. First, these orbitals are not directed in a particular direction; instead, they tend to spread out in all directions (or at least two directions). Second, to the extent that the orbitals have an orientation (the px along the x axis, for example), the geometry is often inconsistent with the molecular geometry. For example, in methane (CH4) the carbon is at the center of the molecule and the hydrogens lie on the points of a tetrahedron. Each H-C-H bond angle is 109.5o. The carbon 2s orbital is spherical and as such extends toward all four hydrogen atoms. The carbon 2px, 2py, and 2pz extend along the x, y, and z axes and as such form 90o angles with each other.
The solution to this problem is to create a new set of atomic orbitals. Consider the valence shell of a carbon atom. The basic 2s, 2px, 2py, and 2pz wave functions are mathematically combined to obtain a new set of atomic orbitals. The new orbitals are called hybrid orbitals. The hybrid orbitals are constructed to have geometries that match the geometry of the molecule. The hybrid orbitals have energies intermediate between those of the basic orbitals used to construct them. Basic atomic orbitals not employed in constructing hybrid orbitals are unaffected by the hybridization process.
sp Hybrid Orbital
Consider the carbon dioxide molecule. The molecule is linear with a O-C-O bond angle of 180o. Valence Bond Theory requires two orbitals on the carbon atom that can be used to form sigma bonds with the two oxygens. One hybrid orbital provides direct overlap with an orbital on one oxygen atom; the other hydrid orbital provides direct overlap with an orbital on the other oxygen atom.
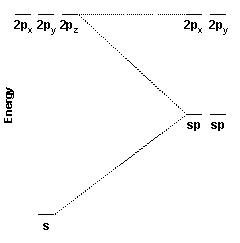
These two hybrid orbitals, the sp hybrid orbitals, are constructed from the carbon 2s and 2pz orbitals. Because two atomic orbitals were used to create the hybrid orbitals, two hybrid orbitals are formed. One sp hybrid orbital is oriented along the positive z axis; the other is oriented along the negative z axis.
The energy diagram for the hybridization process is shown at the right. Notice that the 2px and 2py orbitals are unaffected while the 2s and 2pz orbitals are been converted into two new degenerate orbitals of intermediate energy.
sp2 Hybrid Orbital
Consider the carbonate ion. The O-C-O bond angle in CO32- is 120o; the molecule is perfectly planar. Valence Bond Theory requires three orbitals on the carbon atom that can be used to form sigma bonds with the three oxygens. For each oxygen atom, there is one sp2 hybrid orbital on the oxygen that provides direct overlap with an orbital on the oxygen atom.
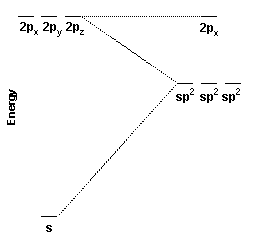
These three hybrid orbitals, the sp2 hybrid orbitals, are constructed from the carbon 2s, 2px, and 2py orbitals. Because three atomic orbitals were used to create the hybrid orbitals, three hybrid orbitals are formed. One sp2 hybrid orbital is oriented along the positive x axis, one is oriented 120o to the lower left, and the other is oriented 120o to the upper left.
Other Hybrid Orbital
Other sets of hybrid orbitals can be constructed to accomodate other geometries. The table below provides a list of common geometries and sets of hybrid orbitals having this geometry.
| Geometry | Hybrid Orbitals | Number of Orbitals | Atomic Orbitals used to form Hybrid Orbitals |
|---|---|---|---|
| linear | sp | 2 | s, pz |
| trigonal planar | sp2 | 3 | s, px, py |
| tetrahedral | sp3 | 4 | s, px, py, pz |
| trigonal bipyramidal | dsp3 | 5 | s, px, py, pz, dz2 |
| octahedral | d2sp3 | 6 | s, px, py, pz, dz2, dx2-y2 |
| square planar | dsp2 | 4 | s, px, py, dx2-y2 |
The electron density plots below compare the sp, sp2, and sp3 orbitals. Notice that these orbitals are all very similar, in that the majority of the orbital is oriented in a particular direction.
Hybrid orbitals based on d orbitals are only possible for elements in the third or higher row, and the structures of these orbitals are more complicated.
The sp3d hybrid orbitals, which taken together have trigonal bipyramidal geometry, are somewhat unusual in that not all orbitals are identical. The axial orbitals, which are oriented along the z axis, are different from the equitorial orbitals, which lie in the xy plane.
HybridOrbitals.html version 3.0
© Copyright 2000, 2014, 2023 David N. Blauch