Chemical Equilibria
Basic Concepts
Consider the following gas-phase chemical reaction:
H2 + I2 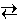 2 HI
2 HI
Imagine a small mixing chamber into which gaseous H2 and I2 are rapidly introduced. Initially there is no HI, H2 is present at 0.020 M concentration, and I2 is present at 0.024 M concentration. As time goes by, however, the hydrogen and iodine react to form HI, as shown in the simulation below.
Click on the Start Simulation button and observe how the concentrations of the three compounds change with time.
As the reaction progresses, the concentrations of iodine and hydrogen decrease as they are consumed while the concentration of hydrogen iodide increases as it is formed. Eventually, however, the concentrations of all three species reach constant values. This behavior results from the back reaction in which hydrogen iodide reacts to form iodine and hydrogen. Initially there is no hydrogen iodide, so the back reaction cannot occur. As hydrogen iodide accumulates, the back reaction becomes significant.
Eventually the rate at which iodine is consumed by the forward reaction is perfectly balanced by the rate at which it is produced by the back reaction. The same is true for hydrogen and hydrogen iodide. When the rates of forward and reverse reactions are perfectly balanced in this way, the reaction is said to be at equilibrium.
Even though the concentrations of the various chemical species do not change at equilibrium, the forward and reverse chemical reactions continue to occur. For this reason we describe chemical equilibrium as a dynamic process.
The Law of Mass Action
When a chemical reaction reaches equilibrium, the concentrations of the reactants and products obey the Law of Mass Action.
For the generic chemical reaction
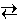 c C + d D
c C + d D the Law of Mass Action is
The uppercase letters represent chemical species while the lowercase letters represent the corresponding stoichiometric coefficients. The notation [A] represents the molar concentration of species A.
In this expression, the numerator contains the concentration of each product raised to the power of its stoichiometric coefficient. The denominator contains the corresponding expression for the reactants.
If the species are gases, an entirely analogous expression may be written using partial pressures instead of molar concentrations.
The equilibrium constant KC applies to an equilibrium expression written in terms of molar concentrations, and the equilibrium constant KP applies to an equilibrium expression written in terms of partial pressures.
One can convert between KC and KP using the ideal gas law.
For example: PA = R T [A]
The equilibrium constant characterizes the "position" of the equilibrium. The larger the equilibrium constant, the more the equilibrium favors products. The smaller the equilibrium constant, the more the equilibrium favors reactants. In an ideal system, the equilibrium constant depends only upon the temperature of the system.
Note: Only species that are gases or solutes appear in the equilibrium expression.
Pure solids and pure liquids do not appear in the expression.
When solutes are involved, one always uses molar concentrations for the solutes.
BasicConcepts.html version 3.0
© 2000, 2014, 2023 David N. Blauch