Molecular Dynamics Simulation: The Gas Phase
Statistical mechanics envisions matter as being composed of a large number of small particles in rapid motions.
A simulation of this behavior is provided below. This simulation, called Molecular Dynamics, applies Newton's laws of motion
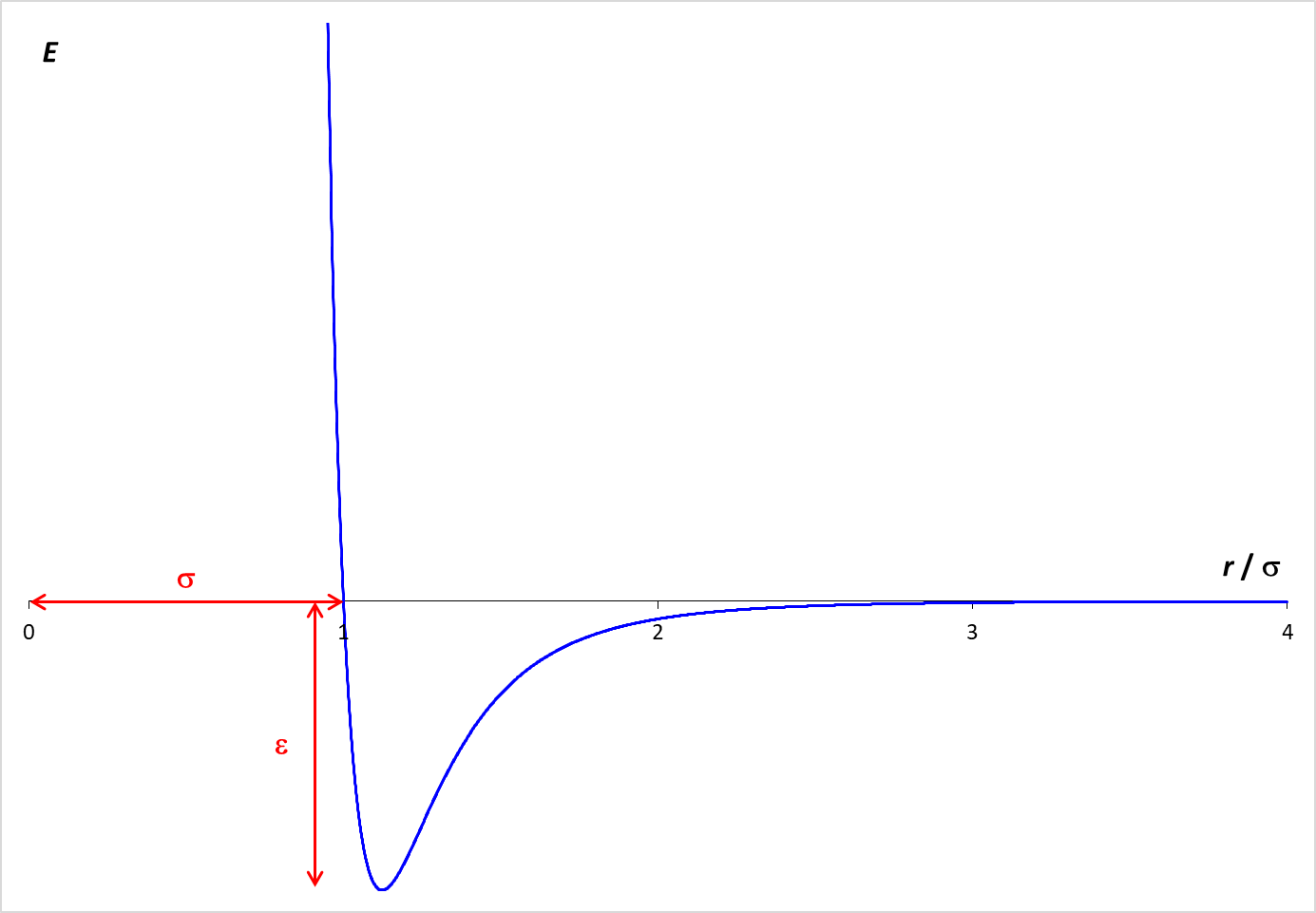
to predict the paths of individual particles or molecules, represented by the red balls. The forces that operate on the particles are described by the Lennard-Jones potential,
which is graphed at the right. The graph shows how the potential energy (PE) arising from the interaction of two particles varies with the distance (r) between the particles.
When the molecules are far apart, the PE is essentially zero.
As the molecules get closer, there is an attractive force between the particles, which lowers the PE. The particles need to be fairly close for this attraction to be relevant. In the simulation, the particle diameter is σ. Examination of the graph shows that the particles need to be within about two diameters (2 σ ) for a significant attractive force to exist. If the molecules get too close (within one diameter), however, the PE increases rapidly. This strong repulsive force drives particles away from each other and is the reason why the particle "bounce" off each other.
The depth of the Lennard-Jones energy well is ε which is 1.0 kJ/mol in this simulation.
When the molecules are far apart, the PE is essentially zero.
As the molecules get closer, there is an attractive force between the particles, which lowers the PE. The particles need to be fairly close for this attraction to be relevant. In the simulation, the particle diameter is σ. Examination of the graph shows that the particles need to be within about two diameters (2 σ ) for a significant attractive force to exist. If the molecules get too close (within one diameter), however, the PE increases rapidly. This strong repulsive force drives particles away from each other and is the reason why the particle "bounce" off each other.
The depth of the Lennard-Jones energy well is ε which is 1.0 kJ/mol in this simulation.
Questions
Run this simulation of a gas, observe the behavior of the molecules, and answer the following questions.- What features are characteristic of the gas phase?
- On average, are the molecules close together or far apart?
- Does the gas phase have a rigid shape?
- Does every molecule freely move to all regions of the container?
- Does the gas have its own rigid shape or does it expand to fill the entire container?
- Describe how the molecules move.
- Do all the particles move at the same speed?
- What is the effect of changing the temperature on the behaviour of the particles?
- Describe the interactions between molecules.
- Do any of the particles stick together? Explain this observation.
- Is the average potential energy positive or negative? Explain the significance of the sign of the potential energy.
- Is the magnitude of the average potential energy relatively small or large? Explain why.
Molecular Dynamics - The Gas Phase (MDS-Gas.html, version 1.0)
© 2020 David N. Blauch