Vapor Pressure
Concepts
A phase change may be written as a chemical reaction. The transition from liquid water to steam, for example, may be written as
H2O (l) 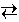 H2O (g)
H2O (g)
The equilibrium constant for this reaction (the vaporization reaction) is
where Pw is the partial pressure of the water in the gas phase when the reaction is at equilibrium. This pressure is often called the vapor pressure.
This equilibrium may be established at any temperature. Because vaporization reactions are endothermic, an increase in temperature will shift the equilibrium to the right. Thus at low temperatures the vapor pressure of the liquid is very low and at high temperatures the vapor pressure is quite large.
At what temperature will the liquid boil?
The boiling point corresponds to the temperature at which the vapor pressure of the liquid equals the atmospheric pressure. If the liquid is open to the atmosphere (that is, not in a sealed vessel), it is not possible to sustain a pressure greater than the atmospheric pressure, because the vapor will simply expand until its pressure equals that of the atmosphere.
The temperature at which the vapor pressure exactly equals one atm is called the normal boiling point.
In a sealed vessel, where the vapor cannot expand and thus the pressure can build up, it is possible to establish the vaporization equilibrium at temperatures in excess of the normal boiling point.
The van't Hoff equation provides a relationship between an equilibrium constant and temperature.
For this reaction, the equilibrium constant is simply the vapor pressure, Pw, which when substituted into the above equation yields the Claussius-Clapeyron equation.
The normal boiling point, Tbp°, corresponds to the temperature at which both the reactant and the product are in the standard state. A pure liquid under 1 atm pressure is in the standard state. A pure gas at 1 atm pressure is also in the standard state. Thus in the standard state Pw = 1 atm. The consequence is that the normal boiling point is related to the standard enthalpy of vaporization and the standard entropy of vaporization:
This relation allows the Claussius-Clapeyron equation to be rewritten as
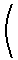
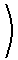
As these equations illustrate, experiment data for the vapor pressure of a liquid as a function of temperature enables the calculation of both the normal boiling point, the standard enthalpy of vaporization, and the standard entropy of vaporization.
Experiment
Objectives
- Determine the standard enthalpy of vaporization for ethanol.
- Determine the standard entropy of vaporization for ethanol.
- Determine the normal boiling point for ethanol.
The experimental equipment shown below consists of a glass bulb connected to a manometer. (The bulb and manometer are shown, but not the connecting tube.) The bulb is evacuated (that is, a vacuum pump is employed to remove all the gas inside the bulb) and a small amount of liquid ethanol is added. The bulb and manometer constitute a closed system containing liquid ethanol and gas-phase ethanol. Thus the pressure measured by the manometer is the ethanol vapor pressure.
The temperature of the bulb and manometer can be varied. Use the Heat and Cool controls to change the temperature. As the temperature changes, the vapor pressure of ethanol changes. The manometer may be used to measure the pressure at any temperature. The pressure-temperature data is automatically plotted on the graph at the right.
Record at least five data points (temperature and pressure) over the temperature range 0 to 50°C. A plot of ln P vs 1/T is created and the line-of-best-fit is plotted through the data. Note that the absolute temperature (degrees Kelvin) is required in the Claussius-Clapeyron equation. The pressure should be entered with units of atm. Use the slope and intercept of the line-of-best-fit to determine the standard enthalpy of vaporization, the standard entropy of vaporization and the normal boiling point of ethanol.
VaporPressure.html version 3.0
© 2001, 2014, 2023 David N. Blauch