NMR Spectroscopy: Larmor Precession

Nuclear Spin

One of the noteworthy properties of a proton and a neutron is that each has intrinsic angular momentum ( p ) and an intrinsic magnetic moment ( μ ). That is, each particle behaves like a little magnet with a north pole and an opposing south pole. For this reason, μ is a vector: the magnetic moment has a magnitude and a direction in space. ( p and μ are each written in bold to indicate they are vectors.)

The magnitude of the angular momentum, and thus the magnitude of the magnetic moment, is characterized by the nuclear spin ( I ), and both the proton and the neutron have I = ½. The magnetic moment of an atomic nucleus is simply the sum of the magnetic moments of all the protons and neutrons in the nucleus. For ¹H the nucleus is just a proton and thus I = ½ .

For ⁴He there are two protons and two neutrons. The two protons are paired in the same nuclear orbital, with their magnetic moments (north and south poles) opposing and canceling each other. The same is true for the neutrons, leaving ⁴He with no net spin (I = 0) and thus no magnetic moment. Similarly, all of the protons and neutrons are paired in ¹²C, and thus it also has no magnetic moment. However, there is one unpaired proton in ¹³C, leading to I = ½. There is one unpaired proton and one unpaired neutron in ¹⁴N , which produces I = 1. Note that protons and neutrons are distinguishable particles; therefore, there are separate sets of orbitals for protons and for neutrons.

The magnitude of the angular moment depends upon the particle's spin:

| p | = ℏ [ I ( I + 1 )]^½

The physical constant ℏ equals h/2π, where h = 6.626 x 10^-34 J sec is the Planck constant.

The magnetic moment is directly portional to the angular moment

μ = γ p

The proportionality constant ( γ ) is called the magnetogyric ratio. Each nucleus has an unique magnetogyric ratio, which has units of sec^-1 T^-1. T = Tesla, a unit of magnetic field strength. The table below lists spin properties for a several nuclei.

Nucleus	Spin	10^-7 γ (sec^-1 T^-1)
¹H	½	26.7522
¹³C	½	6.72828
¹⁴N	1	1.93378
¹⁵N	½	-2.71262
³¹P	½	10.8394

Notice that the magnetic moment of ¹H is four times larger than that of ¹³C, even though both are spin ½ nuclei. For this reason, proton NMR is inherently four times more sensitive than ¹³C NMR. Almost all naturally occurring hydrogen is ¹H. Only 1% of naturally occurring carbon is ¹³C. The combination of different abundances and different magnetogyric ratios results in ¹H NMR being 400 times more sensitive than ¹³C NMR.

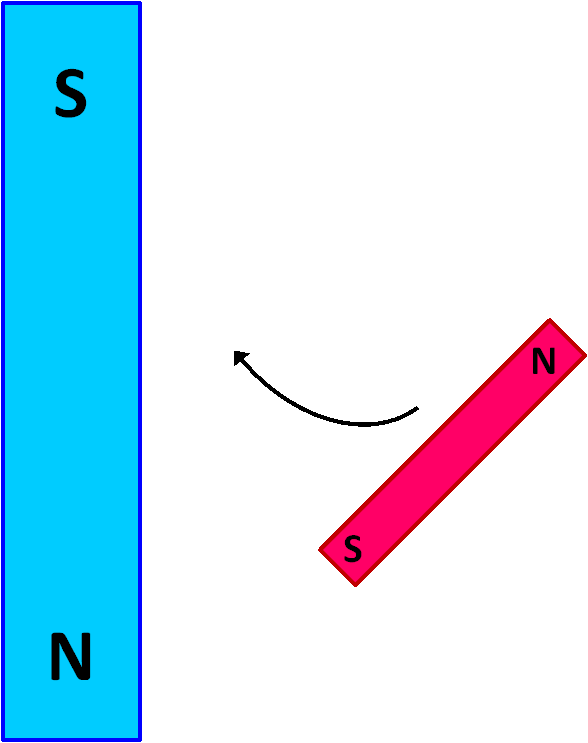
If one obtains a pair of bar magnets and explores how they interact, one will quickly observe that the north pole of one magnet is attracted to the south pole of the other.

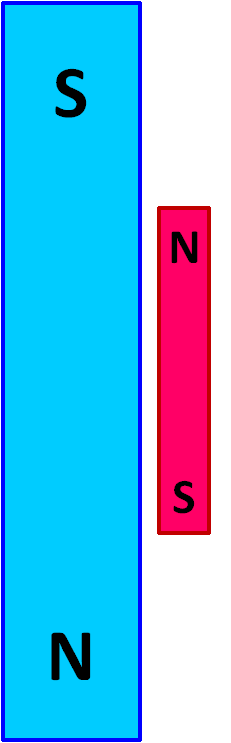
Imagine the large blue magnet in the image at left has a powerful magnetic field ( B ) and is held in a fixed position. The smaller red magnet is free to move. There is a force between the two magnets that will cause the movable red magnet to swing up against the stationary blue magnet in a north-to-south orientation, as shown in the image at the right.

The orientation of the red magnet in the image at the right is the state with lowest energy. Once the system reaches this configuration, it is at equilibrium and no additional change will occur.

Precession

There is a profound difference, however, between the behavior of the macroscopic magnets illustrated above and the magnetic moment of a nucleus. If a nucleus is placed in a stationary magnetic field ( B ) that is aligned along the z axis, the nucleus will attempt to align its magnetic moment against that of B, similar to the bar magnets depicted above. Unlike the bar magnets, however, the alignment of the nuclear magnetic moment with the magnetic field is constrained to discrete levels.

The component of the angular moment (and hence component of the magnetic moment) that can be aligned along the z axis (that is, aligned along B ) is given by the quantum number m_z, which has possible values of -I, -I+1, ... I.

For a spin ½ nucleus like ¹H, the permissible values of m_z are +½ and -½.

μ_z represents the component of the magnetic moment ( μ ) that lies along the z axis. The quantum number m_z determines the value of μ_z .

μ_z = γ p_z = ℏ γ m_z

Because there are only two possible values for m_z , there are only two possible values for μ_z .

The consequence of this quantitization is that the nuclear magnetic moment can never be perfectly aligned with B in the way the bar magnets can become perfectly aligned. There is always a residual component of the nuclear magnetic moment in the xy plane and thus there is always a torque on the nucleus.

Joseph Larmor worked out the mathematical description of this persistent torque on the nuclear magnetic moment. The torque causes the nuclear magnetic moment to precess or rotate about the z axis at a constant rate, as illustrated in the animation shown below. This behavior is called Larmor precession.

For a spin ½ nucleus, m_z = +½ or -½, with +½ being the lower energy state. Both possible states are shown below.

The animation at the bottom of the page shows the nuclear magnetic moment vector (μ) as a red arrow. Start the animation and observe the behavior of μ. In particular, observe the following behaviors.

What happens to the z-component of the magnetic moment (μ_z) as time passes?
How does μ_z depend upon the quantum number m_z?
What is the effect of the torque on the orientation of μ?

Important Note! The frequency of precession on NMR spectrometers is in the MHz to GHz range. Thus the time required for one full rotation is a few nsec or less. Actual Larmor precession is approximately a billion times faster than the simulation shown below.

The coordinate system is shown at the right. In the initial view, the z axis is vertical. The positive x direction is to the lower right and the positive y direction is to the upper right. Initially, the bulk magnetism vector lies in the positive yz plane.